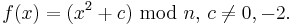Pollard's rho algorithm

Pollard's rho algorithm is a special-purpose integer factorization algorithm. It was invented by John Pollard in 1975. It is particularly effective at splitting composite numbers with small factors.

1 Core ideas
2 Algorithm
3 Variants
4 Application
5 Example factorization
6 Complexity
7 References
8 External links

Core ideas

The rho algorithm is based on Floyd's cycle-finding algorithm and on the observation that (as in the birthday problem) two numbers x and y are congruent modulo p with probability 0.5 after 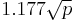$1.177\sqrt{p}$ numbers have been randomly chosen. If p is a factor of n, the integer we are aiming to factor, then 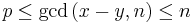$p \le \gcd \left( x-y,n \right) \le n$ since p divides both 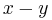$x-y$ and $n$ .

The rho algorithm therefore uses a function modulo n as a generator of a pseudo-random sequence. It runs one sequence twice as "fast" as the other; i.e. for every iteration made by one copy of the sequence, the other copy makes two iterations. Let x be the current state of one sequence and y be the current state of the other. The GCD of |x − y| and n is taken at each step. If this GCD ever comes to n, then the algorithm terminates with failure, since this means x = y and therefore, by Floyd's cycle-finding algorithm, the sequence has cycled and continuing any further would only be repeating previous work.

Algorithm

Inputs: n, the integer to be factored; and f(x), a pseudo-random function modulo n

Output: a non-trivial factor of n, or failure.

x ← 2, y ← 2; d ← 1
While d = 1:
1. x ← f(x)
2. y ← f(f(y))
3. d ← GCD(|x − y|, n)
If d = n, return failure.
Else, return d.

Note that this algorithm may not find the factors and will return failure for composite n. In that case, use a different f(x) and try again. Note, as well, that this algorithm does not work when n is a prime number, since, in this case, d will be always 1.

Variants

In 1980, Richard Brent published a faster variant of the rho algorithm. He used the same core ideas as Pollard but a different method of cycle detection, replacing Floyd's cycle-finding algorithm with the related Brent's cycle finding method.

A further improvement was made by Pollard and Brent. They observed that if 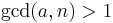$\gcd (a,n) >1$ , then also 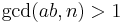$\gcd (ab,n)>1$ for any positive integer b. In particular, instead of computing 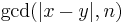$\gcd (|x-y|,n)$ at every step, it suffices to define z as the product of 100 consecutive 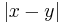$|x-y|$ terms modulo n, and then compute a single 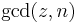$\gcd (z,n)$ . A major speed up results as 100 gcd steps are replaced with 99 multiplications modulo n and a single gcd. Occasionally it may cause the algorithm to fail by introducing a repeated factor, for instance when n is a square. But it then suffices to go back to the previous gcd term, where 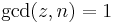$\gcd(z,n)=1$ , and use the regular Rho algorithm from there.

Application

The algorithm is very fast for numbers with small factors. For example, on a 3 GHz workstation, the original rho algorithm found the factor 274177 of the sixth Fermat number (18446744073709551617) in 26 milliseconds; the Richard Brent variant found the same factor in 5 milliseconds. However, for a semiprime of the same size (10023859281455311421), the same workstation using the original rho algorithm took 109 milliseconds to find a factor; the Richard Brent variant took 31 milliseconds.

For f, we choose a polynomial with integer coefficients. The most common ones are of the form:

$f(x)=(x^2%2Bc)\hbox{ mod }n,\,c\neq0,-2.$

The rho algorithm's most remarkable success has been the factorization of the eighth Fermat number by Pollard and Brent. They used Brent's variant of the algorithm, which found a previously unknown prime factor. The complete factorization of F₈ took, in total, 2 hours on a UNIVAC 1100/42.

Example factorization

Let n = 8051 and f(x) = (x² + 1 ) mod 8051.

i	x_i	y_i	GCD(\|x_i − y_i\|, 8051)
1	5	26	1
2	26	7474	1
3	677	871	97

97 is a non-trivial factor of 8051. Other values of c may give the cofactor (83) instead of 97.

Complexity

The algorithm offers a trade-off between its running time and the probability that it finds a factor. If n is a product of two distinct primes of equal length, running the algorithm for O(n^1/4 polylog(n)) steps yields a factor with probability roughly half. (Note that this is a heuristic claim, and rigorous analysis of the algorithm remains open.)

It gets the ρ name because the iteration of the elements looks like a circle with a tail when sketched.

References

Brent, Richard P. (1980), "An Improved Monte Carlo Factorization Algorithm", BIT 20: 176–184, http://wwwmaths.anu.edu.au/~brent/pd/rpb051i.pdf
Cormen, Thomas H.; Leiserson, Charles E.; Rivest, Ronald L. & Stein, Clifford (2001), "Section 31.9: Integer factorization", Introduction to Algorithms (Second ed.), Cambridge, MA: MIT Press, pp. 896–901, ISBN 0262032937 (this section discusses only Pollard's rho algorithm).
Pollard, J. M. (1975), "A Monte Carlo method for factorization", BIT Numerical Mathematics 15 (3): 331–334

External links

Number-theoretic algorithms

Primality tests	AKS · APR · Baillie–PSW · ECPP · Elliptic curve · Pocklington · Fermat · Lucas · Lucas–Lehmer · Lucas–Lehmer–Riesel · Proth's theorem · Pépin's · Solovay–Strassen · Miller–Rabin · Trial division

Sieving algorithms	Sieve of Atkin · Sieve of Eratosthenes · Sieve of Sundaram · Wheel factorization

Integer factorization algorithms	CFRAC · Dixon's · ECM · Euler's · Pollard's rho · p − 1 · p + 1 · QS · GNFS · SNFS · rational sieve · Fermat's · Shanks' square forms · Trial division · Shor's

Multiplication algorithms	Ancient Egyptian multiplication · Karatsuba algorithm · Toom–Cook multiplication · Schönhage–Strassen algorithm · Fürer's algorithm

Discrete logarithm algorithms	Baby-step giant-step · Pollard rho · Pollard kangaroo · Pohlig–Hellman · Index calculus · Function field sieve

GCD algorithms	Binary GCD · Euclidean · Extended Euclidean · Lehmer's

Modular square root algorithms	Cipolla · Pocklington's · Tonelli–Shanks

Other algorithms	Chakravala · Cornacchia · integer relation algorithm · integer square root · Modular exponentiation · Schoof's

Italics indicate that algorithm is for numbers of special forms; bold indicates deterministic algorithm for primality tests (current article is always in bold).